-
Окръжност () - всички точки в една равнина, които са на определено разстояние от дадена точка
а) радиус - отсечка с краища точка и произволна точка от самата окръжност
б) хорда - отсечка с краища две точки от окръжността
- дъга - една от двете части, на които дадена хорда разделя окръжността
Две дъги от една окръжност са равни тогава и само тогава, когато съответните им хорди са равни.
Две хорди в една окръжност са равни тогава и само тогава, когато са на равни разстояния от центъря на окръжността.
Дъгите от една окръжност, заградени между две успоредни хорди, са равни.
в) диаметър - хорда, минаваща през центъра на окръжността
Диаметър на окръжността е перпендикулярен на недиаметрална хорда тогава и само тогава, когато я разполовява.
-
Вписан ъгъл - ъгъл, чийто връх е точка от окръжността, а рамената му пресичат окръжността
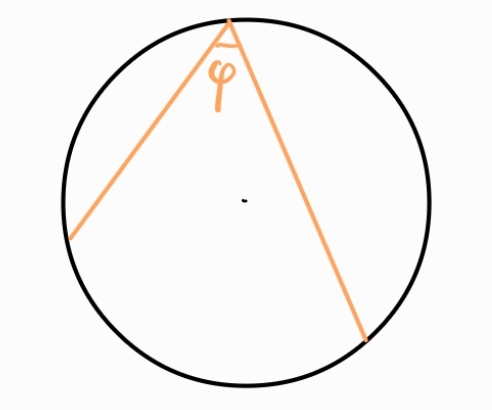
Всеки вписан ъгъл е половината от съответния си централен ъгъл.
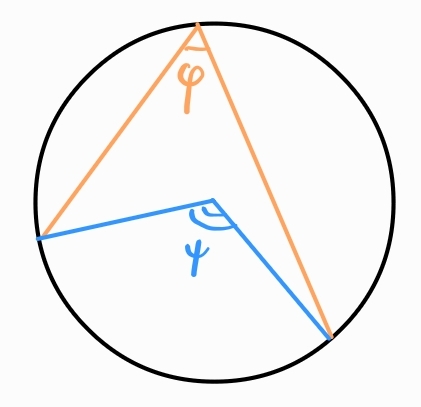
Вписан ъгъл, чиито рамена минават през краищата на диаметър, е прав.
-
Периферен ъгъл - ъгъл, чийто връх е точка от окръжността, едното му рамо е допирателна, а другото я пресича
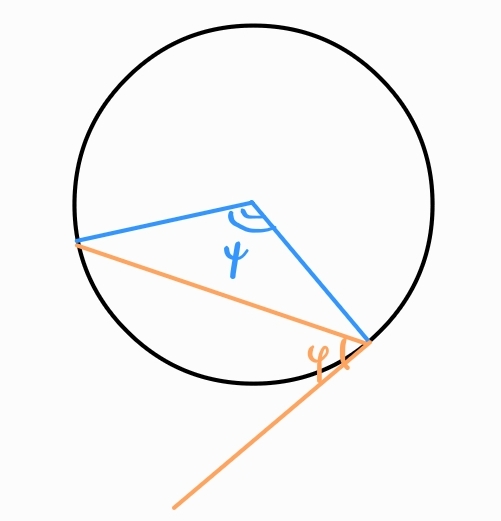
Всеки периферен ъгъл е половината от съответния си централен ъгъл.
Аналитична геометрия на окръжност
-
Канонично уравнение на окръжност
а) център: точката
б) радиус:
-
Обобщен вид на уравнението на окръжност
а) решения - не всяко уравнение от този вид отговаря на окръжност
- няма решения - нито една точка от равнината
- едно решение - окръжността е сведена до единствена точка
- безброй решения - уравнението отговаря на единствена окръжност
б) преобразуване в каноничен вид - възможно само ако уравнението има безброй решения
-
Допирателна към окръжност през точка от окръжността
-
Допирателна към окръжност през точка , която е извън окръжността
Доказателство